Takeaways from last week:Learning:still learning sorry
A sun synchronous orbit needs to orient itself 360 degrees in 365 days, or about 0.9865 degrees /day. This orientation is known as the rate of right ascension, also known as omega_dot. Omega is just the right ascension (see first document for details, and right ascension is a term used to describe how east or west the satellite is orbiting relative to ; the west is the negatvie direction, and east is the positive direction. Declination corresponds to latitude and right ascension to longitude.
tells you oreintation of line, and velocity vector - right ascenion of the ascedning node
if orbit precesses, angle omega will change like a topsy turvy dot - -Capipal Omega - how orbit varies, change in the line interesting
captial omegadot eual to 360 degrees/365 days
little omega - how to positon of the object orbit and changes over tie
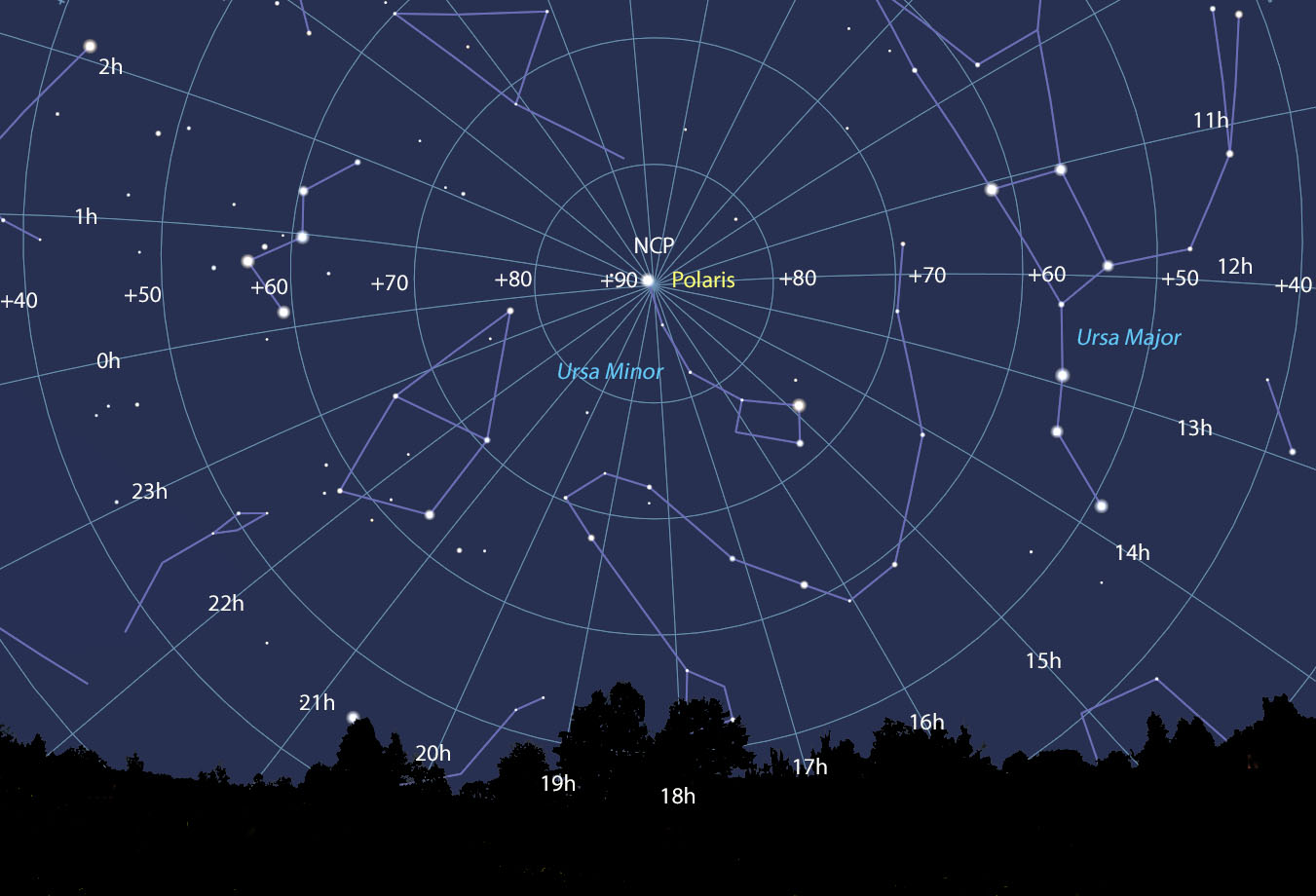
Right ascension is measured from the Sun at the March equinox (vernal equinox) i.e. the First Point of Aries, which is the place on the celestial sphere where the Sun crosses the celestial equator from south to north at the March equinox and is currently located in the constellation Pisces. Right ascension is measured continuously in a full circle from that alignment of Earth and Sun in space, that equinox, the measurement increasing towards the east (positive). The sky can be treated as a clock, since it wheels by as Earth rotates, so the zero point of right ascension is called "0h" for "zero hours." Unlike longitude, right ascension is measured in just one direction — east. Because there are 24 hours in a day, each hour of right ascension measured along the equator equals 1/24th of a circle (360° divided by 24) or 15°. That's a little more than one-half the width of the W-shaped constellation Cassiopeia.
In the blue sky picture above ,this view shows the north celestial pole (NCP) and polar regions. Declinations are labeled every 10° and the hours of right ascension are shown around the circle. By convention, 0h is used instead of 24h.
Each planet has its own J2 value, that is a determination of its oblateness/zonal variability as you move from the squishy equator to the pole. J2 is related to the oblateness, or the roundness of a planet (where 0 is a perfect sphere), and increase in value as you increase oblateness. J2 is different for each planet. Look up J2 for earth
Unlike Earth coordinates, celestial coordinates change due to the slow wobble of Earth's axis called precession. Precession causes the equinox points to drift westward at a rate of 50.3 arcseconds annually. As the equinox shifts, it drags the coordinate grid with it. So we need to precess with it by using a sun synch orbit, orienting our right ascension!
Right ascension is known as omega; rate of right ascneion is known as omega_dot. We need omega_dot to be =
So, ascension is like changing orientation relative to earth equator (say, sun synched orbit around the equator); periapsis is ascending toward the north pole (stretch your hand in front of you, incline hand up and down). Inclination (stretch hand in front of you, rotate your hand left to right). Look at pics above (ascension is like rotating about xy plane, periapsis is like about xz plane, inclination is above yz plane).
equatorial plane is reference plane for all the orbits (0 degrees)
orbit lies in a plane, determined by two angles relative to equatoriral plane - -two angles for circle, three for
rotate about the axis and then tilt it (ascension, then inclination?) - center of earth and orentiation is polar coordinates is declination and right ascension xy and declination is latitude in the sky that you look at it from ; declination locked to latitude; and 0h of right ascencion is noon overhead at vernal equinox ----if this is
define inclination of orbit, then define the right ascension at the ascedning node
right ascension of the ascending node - point on the line that is going south to north where orbit plane and equi. plane intersect ;;; tells you orientation of the plane relative to the equator
do inclination first, then rotate to get the right ascension of the ascnedoing node
mean anomaly - the phase of the orbit ; where it is in the orbit in one orbit
we only care about the rate of change of ascension? do we mode orbits simulating both changes in periapsis and inclination? It looks like that from above, we can put in omega_dot = 15 arcsec/sec and find the a and the i that correspond to that.
if w_dot = omega_dot, would it be kind of like visualizing a topsy-turvy thing like orbit going around the planet (where the cross section of the topsy turvy is the orbit?)
what period- dont care what the period is, it is going to be what it will be; only depedennt on a
scintillation and strobe lighting? -if it turns out that angular rate is too large (too much light) , we could use a flashing image instead of a constant source
scillation - stars twinkle, atmophere is a lens that converges and diverges the beam - -if you take a long enough average you get the avg of tthe source ;; but a strobe would have fluctuations bc not constant
stras are moving at 15 arcsec *cos(declination) ; ideally, we would have the satellite also moving at this rate as the stars ;;;; but this is wrong
center of earh - stars are fixed, ang rate = 0
on the earth - motion of intertia of satellite , parallax (line of sight is moving, the sat is moving across the sky - sate
bottom line: satellite is locked to the stars ; do not compute ;;;;do not calc ang rate from center of earth bc stars fixed
do i have to do negatvie and positive rate of ascension to attain both solutions?
sun synch can mean:
- the a of the ellispse has a fixed angle relative to the sun (a lot of orbits that rotate once a year)
- there are a fraction of those orbits that come over the same part of the earth once every 24 hours (we dont care about this constraint ) – bc the periods we will have are 4 to 5 hours – will eventually catch one of its orbits on a calibrating orbit )
-
how this would look?- blue track (location on earth where it is overhead; red is the next revolution of orbits, green is next
satellite orbit
MTTA - mean time to access - on avg, how long do we have to wait until we can see the next satellite ; depedns on what you contrain the elevation angle ;12 hours (average) - histogram of distributions for this
look at book example is that what we want??
orbit perturbations vary over time, so we should take this into account for 10.93b? oh nmv both are the same equation; they mentioned frozen orbits though?
using poliastro - - so do i just use this instead of wiritng all those equations by hand, i presume?