So, I figured out why fishy numbers were arising in the calculation.
Expectation:
We should expect that when an orbit is put at an inclination of 23 degrees, and the orbit's parameters (a,e,inclination) are set such that the orbit is sun-synchronous, the time spent in the Earth's shadow (for access and observation of the satellite payload) should be the same throughout the year.
In other words, if an orbit is in the plane of the ecliptic, at 23.5 inclination, the satellite should spend some fraction f of its orbit in the Earth’s shadow, independent of time of year.
Problem:
We are not seeing this expectation fulfilled.
Solution:
There is a misunderstanding regarding how the orbit precesses with regard to nodal and apsidal precession.
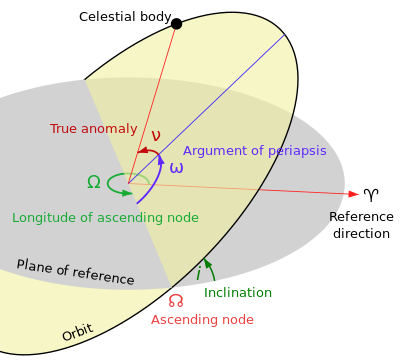
When a orbit is deemed sun synchronous, it's typically in the context of making the nodal precession (or nodal rate regression) equal to 0.98 deg/day, or 360 degrees in a year. With nodal precession, this means that the line of nodes (connecting the ascending and descending node) precesses at the rate given by the equation located above.
Sun-synchronous orbits are always defined in the context given above.
However, changing the parameters a,e, and inclination does not just affect the rate of nodal precession. There is a second type of precession that explains what has been happening to these orbits - apsidal precession. Apsidal precession is the rotation of the line of apsides (line connecting apogee and perigee). The rate of apsidal precession, dw, is given by the equation above.
Apsidal precession and nodal precession can either work with each other or against each other, in that they sum to the total amount of precession an object experiences in one year.
Take